Capillary condensation model

Model description

Both capillary and uniform condensation are modeled with the following equation:

\frac{dV}{dt}=\frac{1}{4}A\alpha v_{\rm T}\frac{Mp_{\rm sat}}{\rho R_{\rm g}T}\left(\nu-\exp\left[\frac{1}{2}\ell_{\rm K}\kappa\right]\right)

where $V$ is condensate volume, $A$ is area of the vapor-liquid interface, $v_{\rm T}$ is thermal velocity, $M$ is molecular weight of the condensate, $p_{\rm sat}$ is saturated vapor pressure of the condensate, $\rho$ is density of the condensate, $R_{\rm g}$ is the universal gas constant, $T$ is temperature, $\nu$ is vapor saturation, $\ell_{\rm K}$ is Kelvin length, $\alpha$ is the molecular accommodation coefficient (assumed to be unity here), and $\kappa$ is the mean curvature of the vapor-liquid interface. Thermal velocity and Kelvin length are given by:

v_{\rm T}=\sqrt{\frac{8R_{\rm g} T}{\pi M}}\quad \ell_{\rm K}=\frac{2\gamma M}{\rho R_{\rm g} T}

Note that condensation is considered on a single primary particle and a single junction. Hence, to get quantitative results, calculated capillary and uniform coating volumes need to be multiplied by the number of primary particles present in the aggregate of interest.

The integration time step $\Delta t$ is computed based on the characteristic condensation rate:

\Delta t=\frac{4\rho R_{\rm g}T}{v_{\rm T}p_{\rm sat}AM\nu}\times C

where $C$ is a constant equal to $10^{-32}\ \rm m^3$ . Hence, the time step is inversely proportional to the characteristic condensation rate and is larger for less volatile materials. Thus, the residence time must be increased when modeling less volatile coatings to ensure that there are enough points to resolve the filling angle vs. time profile.

Coating geometry

If vapor is supersaturated ( $\nu > 1$ ), exceeding a critical value necessary to overcome the Kelvin effect, it can condense on the convex surfaces of the spherical primary particles in an aggregate, thus engaging in “uniform condensation”. Otherwise, condensation is only possible on the concave surfaces between the primary particles. Condensation in those gaps is called “capillary condensation”.

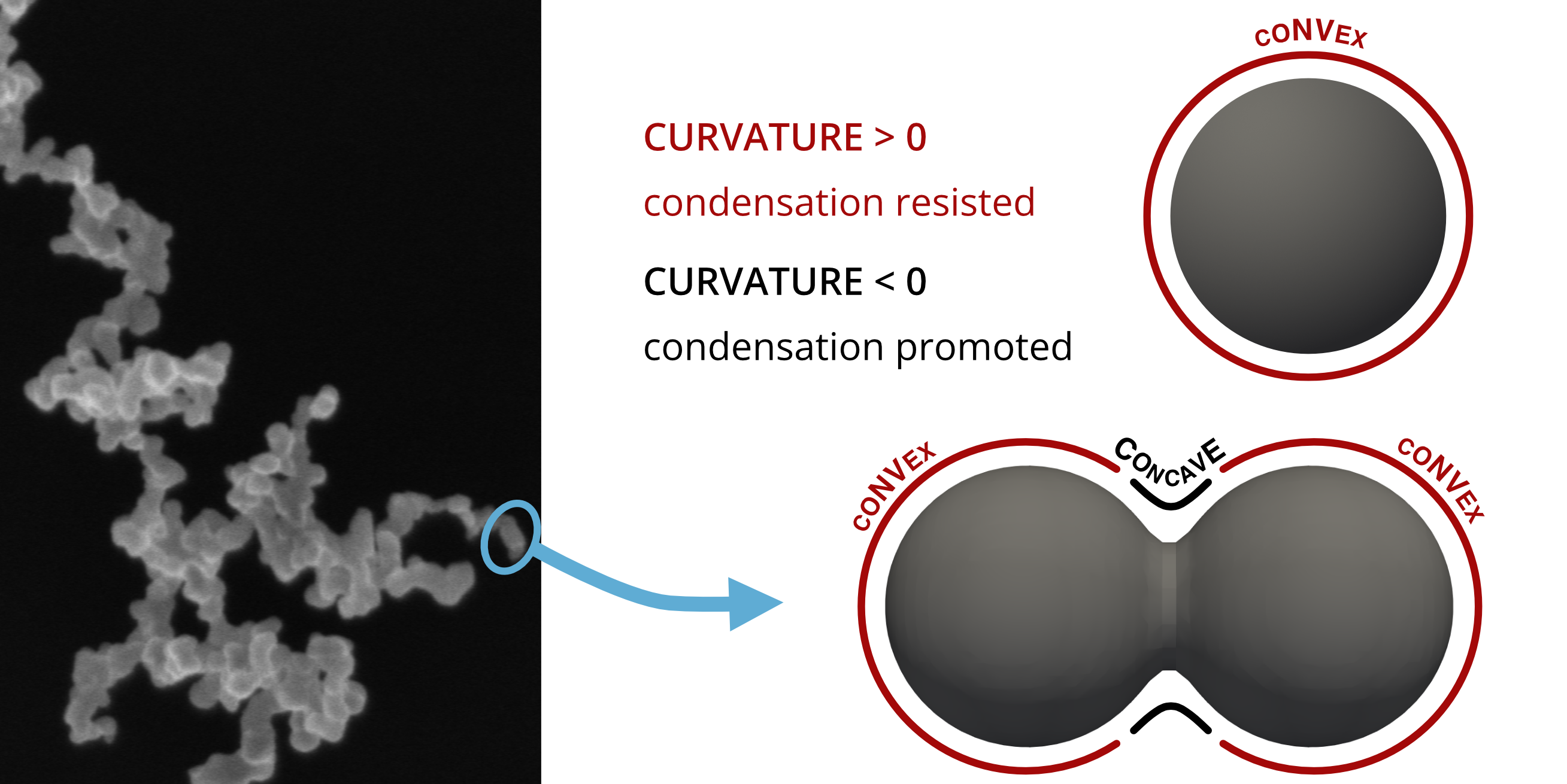
Illustration of convex and concave surfaces

The mode of condensation that will occur in a given system can be estimated using the $\chi$ parameter proposed by Chen et al. ¹:

\chi=\frac{\ell_{\rm K}}{R_{\rm s}}\frac{1}{\nu-1}

If the $\chi$ parameter is close to unity, capillary condensation is expected. If $\chi$ is much lower than one, then both capillary and uniform condensation will occur.

Illustration of capillary only and capillary with uniform condensation modes

The model implemented in this web application considers both possible condensation modes. For the purpose of uniform condensation, condensate on the primary particles is assumed to have a core-shell geometry, and the corresponding area and curvature are used. Geometry of the capillary condensate is more complicated; As described by Ivanova et al. ², condensate in a gap between two primary particles is assumed to be a body with a surface of constant mean curvature. The liquid profile can be obtained by solving the following differential equation:

f''(z)=\left(1+f'^2(z)\right)^{3/2}\left[\frac{1}{f(z)\sqrt{1+f'^2(z)}}-2\tilde\kappa\right]

where $\tilde\kappa$ is mean curvature of the revolution surface non-dimensionalized with the primary particle radius, $\tilde\kappa=R_{\rm s}\kappa$ . The equation becomes a boundary value problem with an unknown parameter, thus requiring three boundary conditions, which are:

f(0)=\sin\theta\quad f'(0)=\tan\left(\theta+\phi-\frac{\pi}{2}\right)\quad f'(1-\cos\theta)=0

where $\phi$ is the contact angle of the coating material. Volume and surface area of the revolution surface can be computed numerically from the $f(z)$ solution. In practice, a table of curvatures, volumes, and surface areas of the constant mean curvature surface is pre-computed for a range of $\theta$ and $\phi$ combinations. Curvatures and areas are then interpolated between available points and scaled by the primary particle radius when solving the condensation equation.

Vapor saturation

Vapor saturation is the main parameter controlling the mode and rate of condensation. The magnitude of saturation depends on the source of condensable vapor. Typically, vapor becomes supersaturated ( $\nu>1$ ) either when it is suddenly cooled or when its volatility is reduced through a chemical reaction. Otherwise, if vapor is in equilibrium with a sink, it is usually subsaturated ( $\nu<1$ ). Thus, methods to estimate saturation will vary based on the system of interest. For example, in a laboratory study of capillary condensation by Khalizov et al. ³, steady-state saturation of triethylene glycol (TEG) in a partially filled tube at room temperature was estimated with finite element modeling to be 0.9.

Preset compounds

Preset compounds available in this application are triethylene glycol (TEG), dioctyl sebacate (DOS), and 78% by weight aqueous solution of sulfuric acid (SA). Additionally, some condensable compounds used in the MOSAIC atmospheric chemistry simulator ⁴ were added as presets. These are lumped compounds representing oxidation products of α-pinene (API1, API2), limonene (LIM1, LIM2), and aromatics (ARO1, ARO2) ⁵.

Technical requirements

A modern web browser with WebAssembly and web worker support and JavaScript enabled is required to run the application. The application should work on both desktop and mobile devices, as long as the web browser is up to date. The application was tested in Safari, Firefox, and Chrome. Note that calculations run on the client side, thus performance will vary between devices. Please, report bugs and suggestions to Egor Demidov at ed242@njit.edu.

Code availability

The capillary condensation model, including support for multi-component systems, was implemented in an open source C++ library. This web application was built with the C++ library compiled into web assembly, which allows C++ code to run in modern web browsers with near-native performance.

Chen, C., Enekwizu, O. Y., Fan, X., Dobrzanski, C. D., Ivanova, E. V., Ma, Y., Gor, G. Y., & Khalizov, A. F. (2018). Single parameter for predicting the morphology of atmospheric black carbon. Environmental Science & Technology, 52(24), 14169-14179. ↩
Ivanova, E. V., Khalizov, A. F., & Gor, G. Y. (2020). Kinetic model for competitive condensation of vapor between concave and convex surfaces in a soot aggregate. Aerosol Science and Technology, 55(3), 302-315. ↩
Khalizov, A. F., Ivanova, E. V., Demidov, E. V., Hasani, A., Curtis, J. H., Riemer, N., & Gor, G. Y. (2024). An unaccounted pathway for rapid aging of atmospheric soot. ChemRxiv, doi.org/10.26434/chemrxiv-2024-gq9sd ↩
Zaveri, R. A., Easter, R. C., Fast, J. D., & Peters, L. K. (2008). Model for simulating aerosol interactions and chemistry (MOSAIC). Journal of Geophysical Research: Atmospheres, 113(D13). ↩
Schell, B., Ackermann, I. J., Hass, H., Binkowski, F. S., & Ebel, A. (2001). Modeling the formation of secondary organic aerosol within a comprehensive air quality model system. Journal of Geophysical Research: Atmospheres, 106(D22), 28275-28293. ↩